1234
of 4

Real Zeros

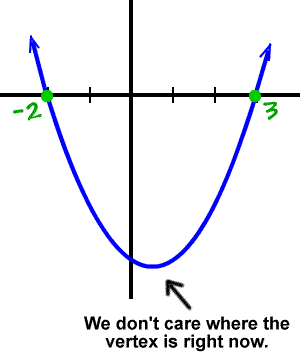
Recall that a real zero is where a graph crosses or touches the x-axis.

Think of some points along the x-axis.

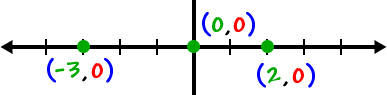
points along the x-axis: ( -3 , 0 ) , ( 0 , 0 ) , ( 2 , 0 )

What are the y values?  0!

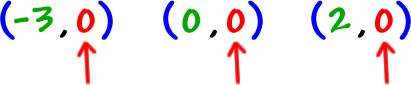
( -3 , 0 ) , ( 0 , 0 ) , ( 2 , 0 ) ... all the y terms are 0

And remember that f(x) is just a fancy function name for y...

So, if we set

f ( x ) = 0  and solve...

  We get the real zeros!

Check it out:

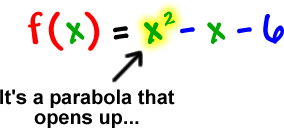
f ( x ) = x^2 - x - 6 ...it's a parabola that opens up

Let's see where it crosses the x-axis:

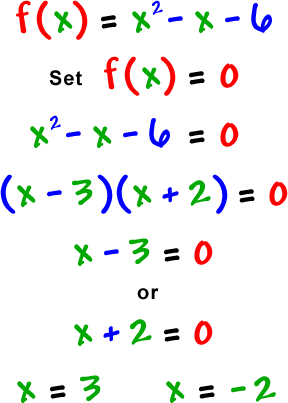f ( x ) = x^2 - x - 6 ... set f ( x ) = 0 , which gives x^2 - x - 6 = 0 which gives ( x - 3 ) ( x + 2 ) = 0 which gives x - 3 = 0 or x + 2 = 0 which gives x = 3 and x = -2

graph of f ( x ) = x^2 - x - 6 ... zeros are -2 and 3 ... we don't care where the vertex is right now

So, the real zeros are

-2 and 3