The Square Root Trick 3

Here's another one done both ways:

WAY 1: Factoring		WAY 2: Square root trick
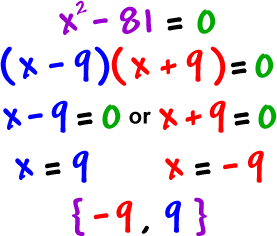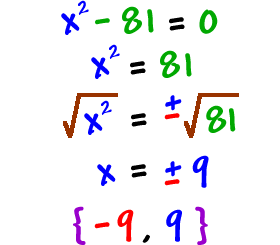$x^2 - 81 = 0 gives ( x - 9 ) ( x + 9 ) which gives x - 9 = 0 or x + 9 = 0 which gives x = 9 or x = -9 ...the solution set is { -9 , 9 }$		$x^2 - 81 = 0 gives x^2 = 81 which gives sqrt( x^2 ) = +/- sqrt( 81 ) which gives x = +/- 9 ... the solution set is { -9 , 9 }$

YOUR TURN:

Solve both ways:

OK, so if we can just factor these things, why do we need the square root trick? Ah, because sometimes you can't factor them!

Check it out:

Solve

Not the difference of two squares, is it?

So, we NEED the square root trick:

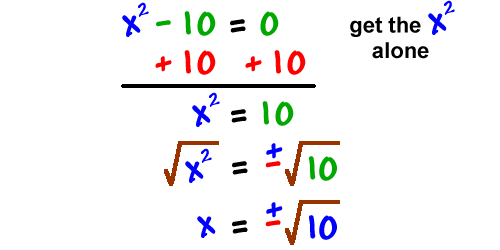
x^2 - 10 = 0 ... get the x^2 alone, which gives x^2 = 10 which gives sqrt( x^2 ) = +/- sqrt( 10 ) which gives x = +/- sqrt( 10 )

of 4