Can we still find the domain and range?
| Domains: |
Yes (as long as the algebra
doesn't get too hairy... and it won't for us.) |
| Ranges: |
Not really (you usually need the
picture -- unless it's something really basic.) |
So, we'll just be doing domains on these -- which is really where the action is anyway.
Asking for the domain of a function is the same as asking
"What are all the
possible x
guys
that I can stick into this thing?"
Sometimes, what you'll really be looking for is
"Is there anything I CAN'T stick in?"
Check it out:
| Let's find the domain of |
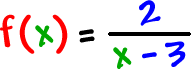 |
Do you see any x guys that would cause a problem here?
| What about |
|
? |
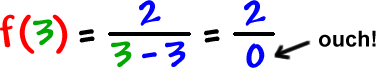
So, x = 3 is a bad guy! Everyone else is OK, though.
The domain is all real numbers except 3.
What would the interval notation be?
When in doubt, graph it on a number line:
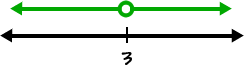
Do the interval notation in two pieces:
| domain |
|
YOUR TURN:
| Find the domain of |
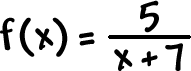 |
Sometimes, you can't find the domain with a quick look.
Check it out:
| Let's find the domain of |
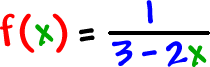 |
Hmm... It's not so obvious!
BUT, we are still looking for the same thing:
 |
The bad
x
that makes the denominator 0! |
How do we find it? Easy!
Set the denominator = 0 and solve!
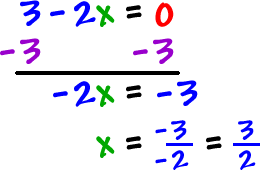
| The domain is |
 |
TRY IT:
| Find the domain of |
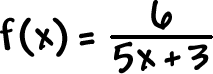 |
*show work!! |
How about this one?
![]()
Square roots -- what do we know about square roots?
![]() ... So, 16
is OK to put in.
... So, 16
is OK to put in.
![]() ... So, 0
is OK.
... So, 0
is OK.
![]() ... Yuck! But,
3.2
is OK.
... Yuck! But,
3.2
is OK.
![]() ... Nope! Can't do it!
... Nope! Can't do it!
*We only want real numbers!
No negatives are OK!

The inside of a radical cannot be negative if we want real answers only (no i guys). So, the inside of a radical has to be 0 or a positive number.
| Set |
|
and solve it! |
Now, let's find the domain of
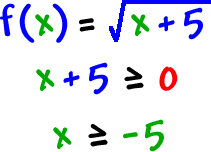
| So, the domain of |
|
is |
|
. |
TRY IT:
| Find the domain of |
|
. *Show work!! |
Here's a messier one:
| Let's find the domain of |
|
Set |
|
and solve! |

| The domain is |
![( -infinity , 7 / 8 ]](/sites/default/files/images/06-functions-25.gif) |
. |
YOUR TURN:
| Find the domain of |
|
. *Show work! |