So, we learned that the more times we compound, the more money we make...  What if we could compound continuously?

Let's figure out how the formula for this would work:

We'll invest $1.00 at 100% interest for one year and we'll keep increasing the compounding and see what happens.

       A quick example, so you can follow this:

$1.00 compounded quarterly at
100% interest for 1 year...

initial amount = $1

split factor = 1.25

number of splits = 4

 

---

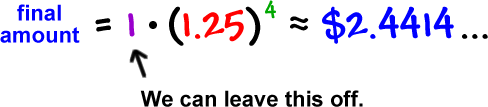
TRY IT:

Do the same for compounded monthly.

---

Let's make a table:

Continued on the next page