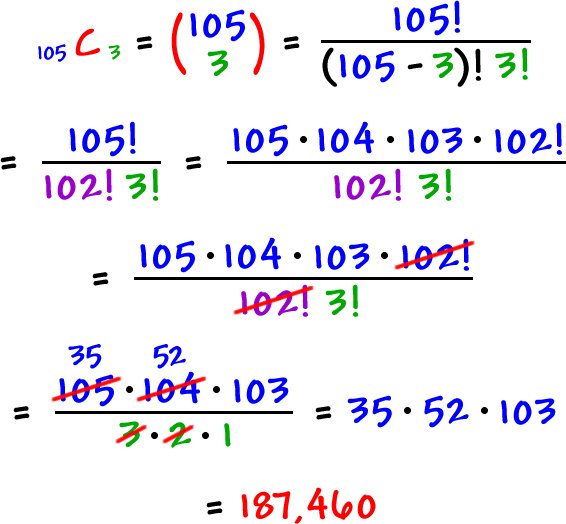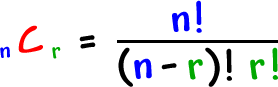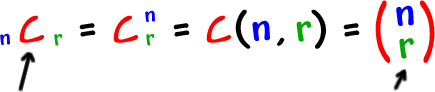1234
of 4

Combinations

Here's the official formula:

The number of ways to CHOOSE n objects
taken r at a time is

n C r = n! / ( n - r )! r!
 

* This can also be phrased as "how many combinations?"

Here are some other notations:

n C r = C n r = C( n , r ) = ( n r )

"C" is for "choose"
(it's really "combinations")

This is NOT
a fraction!

Let's try it!

     You have 105 employees and you need to select a committee of
     3.  How many ways can you do it?

* Ask yourself:  Does order matter?

NO!  So, use the choosing formula.

105 C 3 = ( 105 3 ) = 105! / ( 105 - 3 )! 3! = 105! / 102! 3! = ( 105 * 104 * 103 * 102! ) / 102! 3! ... the 102!'s cancel out ... = ( 105 * 104 * 103 ) / 3 * 2 * 1 ... the 3 * 2 reduces the 105 * 104 to 35 * 52 = 35 * 52 * 103 = 187,460