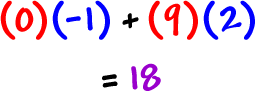Let's use these matrices:
![A = [ row 1: -1 , 5 row 2: 2 , -3 ]](/sites/default/files/images/04-matrices-07.gif) |
|
Let's find ![]() :
:
I do these by stacking... ![]() ...
...
|
|
The answer goes here. |
We just do an intersecting row and column thing:
![A = [ row 1: -1 , 5 row 2: 2 , -3 ] ... B = [ row 1: 0 , 9 row 2: 8 , -6 row 3: 4 , 7 ] ... use column 1 of matrix A and row 1 of matrix B and see where they intersect in the answer matrix c](/sites/default/files/images/04-matrices-13.gif) |
|
![A = [ row 1: -1 , 5 row 2: 2 , -3 ] ... B = [ row 1: 0 , 9 row 2: 8 , -6 row 3: 4 , 7 ] ... 18 goes in c11 of the answer matrix c](/sites/default/files/images/04-matrices-15.gif) |
To fill this spot, we multiply and add:
|
![B = [ row 1: 0 , 9 row 2: 8 , -6 row 3: 4 , 7 ]](/sites/default/files/images/04-matrices-08.gif)
![A is [ row 1: -1 , 5 row 2: 2 , -3 ]](/sites/default/files/images/04-matrices-11.gif)
![B is [ row 1: 0 , 9 row 2: 8 , -6 row 3: 4 , 7 ] ... place an empty matrix of size m x p next to matrix B and below matrix A](/sites/default/files/images/04-matrices-12.gif)