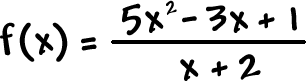OK, so what about this
one?
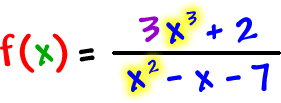
| If we look at |
 |
, we find that the |
|
WILL divide in... |
| But, there's going to be some x stuff left over to deal with. This is when you need to start in with some long division... and we get to ignore the remainder! | ||||

You can stop here
since the rest will be remainder stuff.
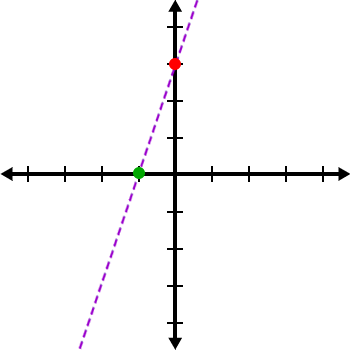
TRY IT:
Find the slant asymptote of