There's another limit thing we geeks get excited about with these graphs -- and it has to do with what happens to the graph around those asymptotes.  We just love following the arrows on graphs.  It's how we spend our Friday nights.

Check it out:

Let's look at this guy again:

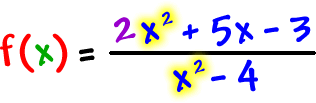
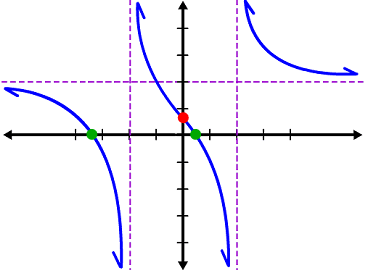
Here's a question for you:

Pierre is running towards x = 2...  What's happening to his altitude as he's approaching?  Does he need scuba gear?  Mountain climbing equipment?

Hmm...  You should now be asking me a question:

From which way is he approaching?  The right or the left?

 

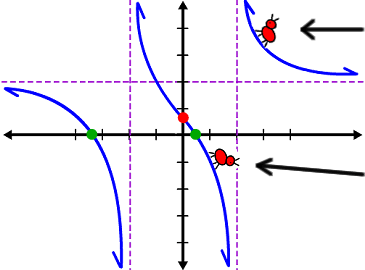If he's climbing in from the right, he's climbing up, up, up. If he's coming in from the left, he's climbing down, down, down.