1234
of 4

The Difference Quotient Review

Writing outf( blob )is what will save you on these!

 

Now, let's dof( x + h ):

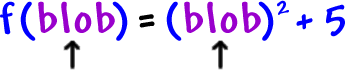
f( blob ) = ( blob )^2 + 5
Just stick x + h in here!
 

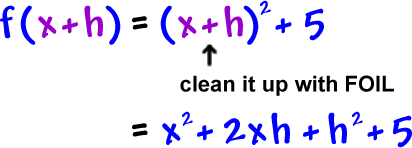
f( x + h ) = ( x + h )^2 + 5 ... clean it up with FOIL ... = x^2 + 2xh + h^2 + 5

 

That wasn't too bad, was it?  Now, can we do the whole difference quotient?

( f( x + h ) - f( x ) ) / h
 

We have the pieces: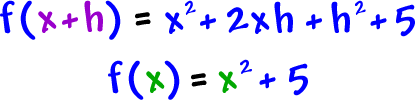

f( x + h ) = x^2 + 2xh + h^2 + 5 ... f( x ) = x^2 + 5

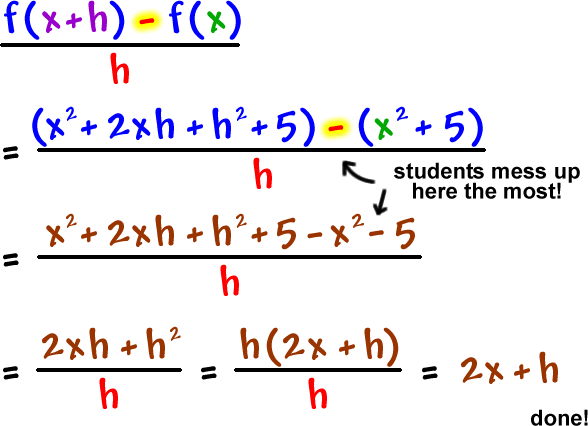
( f( x + h ) - f( x ) ) / h = ( ( x^2 + 2xh + h^2 + 5 ) - ( x^2 + 5 ) ) / h ... students mess up here the most! ... = ( x^2 + 2xh + h^2 + 5 - x^2 - 5 ) / h = ( 2xh + h^2 ) / h = ( h( 2x + h ) ) / h = 2x + h ... done!
 

NOTE:  If you do these difference quotient guys properly, the original h in the denominator will reduce out!