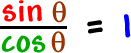123
of 3

Solving Trig Equations

One more:

Solve tan( 3x ) = 1
 
Remember the game on these...  We know how to solve
tan( theta ) = 1 ...  So, let's do that.

 

tan( theta ) = 1 This 1 means that sine and cosine are the same!
 
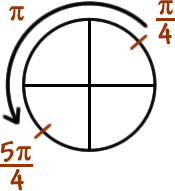start at pi / 4 ... go around pi ... 5 * pi / 4

sin( theta ) / cos( theta ) = 1

So,
 		 theta = ( pi / 4 ) + k * pi
Just go pi around and you pick up the other one.

But, we needed to solve for x, not theta.  Stick the 3x back in for the theta:

theta = ( pi / 4 ) + k * pi ... 3x = ( pi / 4 ) + k * pi ... divide by 3 ... x = ( pi / 12 ) + ( k * pi / 3 )

You can always check this solution on a graphing calculator by graphing

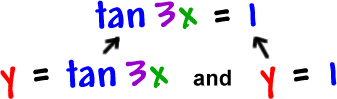
tan( 3x ) = 1 ... y = tan( 3x ) and y = 1
 

at the same time.  They should intersect at x = ( pi / 12 ) and every
pi / 3 interval from there.        

 

TRY IT:

Solve cos( 3x ) = square root( 3 ) / 2