12
of 2

Solving by Graphing

Here's another one:

x + 2y = -2

3x - 2y = -6

Graph them!

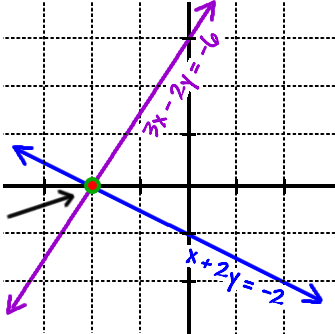
Well, it LOOKS like they intersect at ( -2 , 0 ).  But, what if it's really
( -1.999 , 0.001 ) ? 

We have to check to be sure!

 the graph of x + 2y = -2 and 3x - 2y = -6 ... they appear to cross at ( -2 , 0 )

x + 2y = -2 ... -2 + 2 ( 0 ) = -2

3x - 2y = -6 ... 3 ( -2 ) - 2 ( 0 ) = -6

Yep!  So, the answer is ( -2 , 0 )  .

 

TRY IT:

Solve by graphing:

x - y = 5

3x + 2y = 0

 

This is a cool method for getting you to see what's going on.  But, it has serious problems.

What if you get a graph like this?

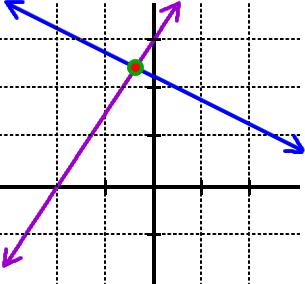the graph of two lines that cross at an indeterminate point What's the answer?

Uh... ( - .4 , 2.3 ) ?
( - .41 , 2.29 ) ?

There's no way to tell.

So, unless the problem is designed to cross at a nice, clean point, the graphing method is pretty useless for solving systems.