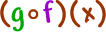| We can flip this all around too! We've been finding | |||
| which is | ... | ||
But, if that wasn't exciting enough (try to calm down), we can find
![]()
(Oh, boy! Oh, boy!)
Check it out:
| Given | and |
| Let's find |
| ... which is |
|
![]()
![]()
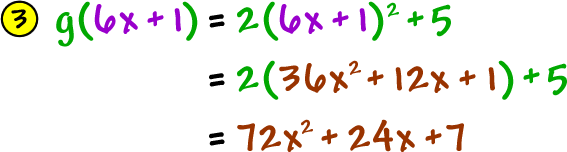
| We found | 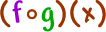 | before: |
![]()
| and |
| Notice that |
| ! |
Usually, you WILL get two different things.
That's why it's so important to read the notation the right way... or you may end up doing it backwards!
Preview: If two functions are inverses of each other, you WILL get
the same thing for both!