1234
of 4

Solving Exponential Equations

Well, in addition to killing e's, he has one more magical power...

He can move the t out of the exponent!

Ln( 3^( t ) ) ... Ln( 3^( t ) ) = t Ln( 3 ) ... the t goes in front of the Ln

OK, repeat after me, "Duuuuuude."

Here's the official rule:

log to the base a( x^( p ) ) = p log to the base a( x )

This works for logs of any base!

Back to our problem:

Remember... 
Anything we do to one side of an equation,
we have to do to the other!

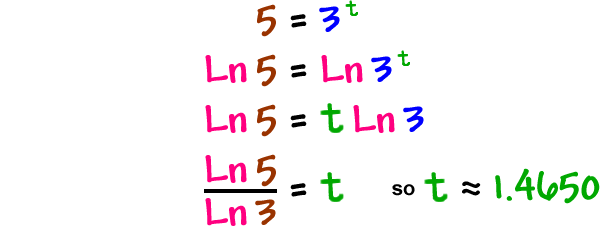
5 = 3^( t ) ... Ln( 5 ) = Ln( 3^( t ) ) ... Ln( 5 ) = t Ln( 3 ) ... Ln( 5 ) / Ln( 3 ) = t ... so t = approximately 1.4650
 

YOUR TURN:

2 = 7^( t )

 

15 = 5 * 6^( t )

* clear the path!