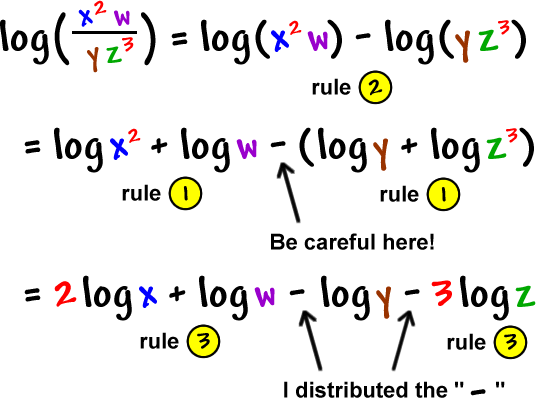1234
of 4

Tricks to Help with Solving Log Equations

Here's how you can use these in Calculus to make your life a lot easier:

Check this guy out:

                                                    Ln( xwz / y^( 2 ) ) ... this is a bit of a mess.
 

Having logs of little things will be much easier, so let's use our rules:

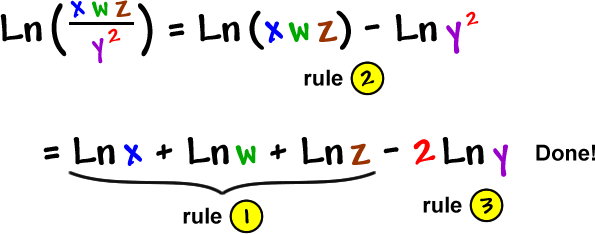
Ln( xwz / y^( 2 ) ) = Ln( xwz ) - Ln( y^( 2 ) ) ... rule 2 ... = Ln( x ) + Ln( w ) + Ln( z ) - 2 * Ln( y ) ... the first three terms are rule 1 ... the last term is rule 3 ... Done!

Trust me on this -- the Calculus on this would take about 10 seconds!
 

Let's do another one:

log( x^( 2 ) * w / y * z^( 3 ) ) = log( x^( 2 ) * w ) - log( y * z^( 3 ) ) ... rule 2 ... = log( x^( 2 ) ) + log( w ) - ( log( y ) + log( z^( 3 ) ) ... the part outside the parenthesis is rule 1 ... the part inside the parentheses is rule 1 ... Be careful here! ... = 2 * log( x ) + log( w ) - log( y ) - 3 * log( z ) ... both parts of this equation are rule 3 ... I distributed the " - "