Here's the cool thing:  We're NOT going to have to keep making these tables!  Since all arithmetic sequences behave the same way (change by adding a number), we can get a formula that works for ALL of them!

Check out the pieces of our last guy:

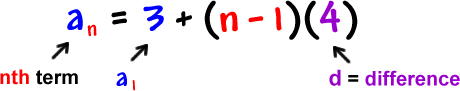
Let's check to see if this thing works on another arithmetic sequence:

How about this guy?

This would be the formula:

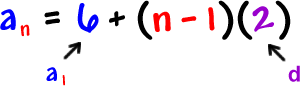
Let's use it to find

:

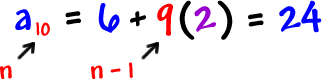
Now, let's check it the long way:

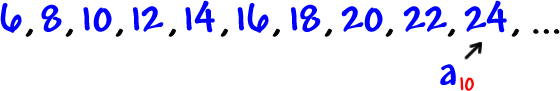
Yep!

The cool thing is that you can use this formula to find the 2000th term: