1234
of 4

Complex Zeros

Let's try another one:

Find the zeros of

f ( x ) = x^4 - 16

then draw a rough sketch of the graph:

What's his basic shape?

x^4 ... basic 4th degree polynomial shape

Let's find those zeros!  How many will there be?  Four, baby, FOUR!  Not 3...  not 5...  4!

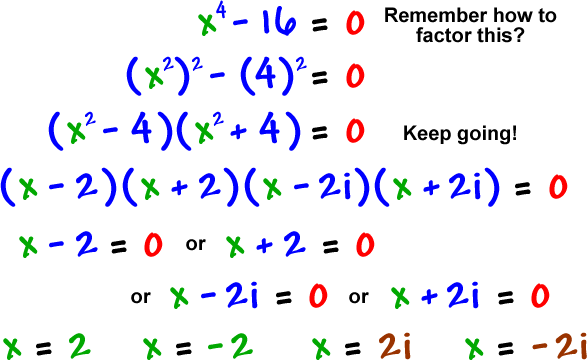
x^4 - 16 = 0 ... remember how to factor this? ... ( x^2 )^2 - ( 4 )^2 = 0 gives ( x^2 - 4 ) ( x^2 + 4 ) = 0 ... keep going! ... ( x - 2 ) ( x + 2 ) ( x - 2i ) ( x + 2i ) = 0 gives x - 2 = 0 or x + 2 = 0 or x - 2i = 0 or x + 2i = 0 which gives x = 2 , x = -2 , x = 2i , and x = -2i

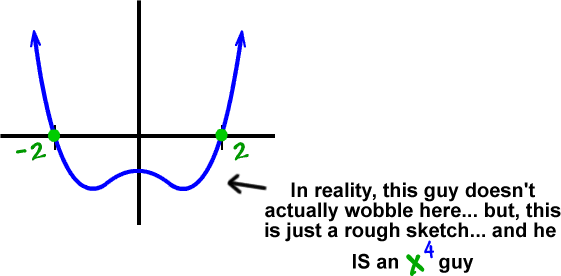
real zeros:  -2 , 2  (shoot throughs)

complex zeros:  -2i , 2i

rough sketch of f ( x ) = x^4 - 16 ... in reality, this guy doesn't actually wobble here... but, this is just a rough sketch... and he IS an x^4 guy

YOUR TURN:

Find the zeros of the following functions, then draw a rough stetch of the graph

f ( x ) = x^5 - 8x^3 - 9x

f ( x ) = -x^4 - 14x^2 - 45