1234
of 4

Types of Zeros

OK, here's a question for you:

Let's say that you've got a mystery 3rd degree polynomial and two of its zeros are 3 and 5i.  Can you find this mystery polynomial?

Well, first of all, it's a 3rd degree guy...  So he must have 3 zeros...  We have two of them.  But, wait?  Someone sure looks lonely! 
The 5i needs his conjugate buddy!

-5i is the other zero!

Now, just work backwards...

Our last step would have been

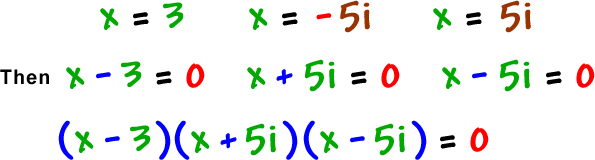
x = 3 , x = -5i , x = 5i , then x - 3 = 0 , x + 5i = 0 , x - 5i = 0 which gives ( x - 3 ) ( x + 5i ) ( x - 5i ) = 0

So

f ( x ) = ( x - 3 ) ( x + 5i ) ( x - 5i ) gives f ( x ) = ( x - 3 ) ( x^2 + 25 ) which gives f ( x ) = x^3 - 3x^2 + 25x - 75

TRY IT:

You have a 4th degree mystery polynomial that has zeros of 3i and
-i ...  What is it?