12
of 2

Absolute Maximums and Minimums

Check out the graph of this guy:

f ( x ) = ( x - 2 )^2 on [ 1 , 4 )

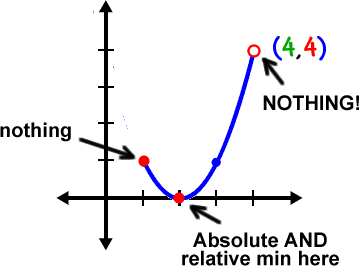
graph of f ( x ) = ( x - 2 )^2 on [ 1 , 4 ) ... the point ( 1 , 1 ) is nothing, the point ( 2 , 0 ) is an absolute and relative min, and the point ( 4 , 4 ) is nothing

f has an absolute and relative min of 0 at x = 2.

So...  why is that (4, 4) point nothing?  Why isn't there an absolute max there?  Well, y = 4 isn't included, so, what would the max be?

3.9?

3.99?

3.999999?

See the problem?

Open endpoints can't be absolute extrema.
 

YOUR TURN:

Find the relative and absolute extrema of:

f ( x ) = | x - 1 | - 3 on ( 0 , 4 ]

(Yes, you need to graph it!)

f ( x ) = 4 - x^2 on [ -2 , 2 ]