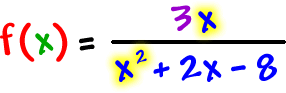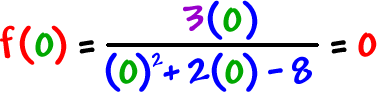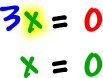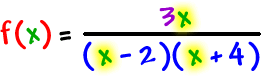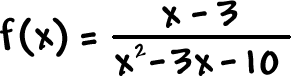123
of 3

Putting It All Together

Let's do another one:

Graph
 

f ( x ) = ( 3x ) / ( x^2 + 2x - 8 )
 

2 things
and
2 sentences!
 

1
 

The y-intercept: Find f(0)
 

f ( 0 ) = ( 3 ( 0 ) ) / ( ( 0 )^2 + 2 ( 0 ) - 8 ) = 0

( 0 , 0 ) ... nowhere else

 

2
 

The x-intercept: numerator = 0, solve
 

3x = 0 gives x = 0

 

( 0 , 0 ) ... nowhere else
 

3
 

Vertical asymptotes: denominator = 0, solve
 

x^2 + 2x - 8 = 0 gives ( x - 2 ) ( x + 4 ) = 0 which gives x = 2 and x = -4
 

The lines x = -4 and x = 2
 

4
 

Horizontal asymptote:
 

Look at
 

( 3x ) / ( x^2 )
 

The line y= 0

arrow                   

*When this is the case, we're going to be forced to "quickie plot" a few points to nail the graph.  No, this is not being a sissy -- we'll have no choice.  Calculus will take care of this though!

OK, let's start graphing!

Let's get our intercepts and asymptotes down:

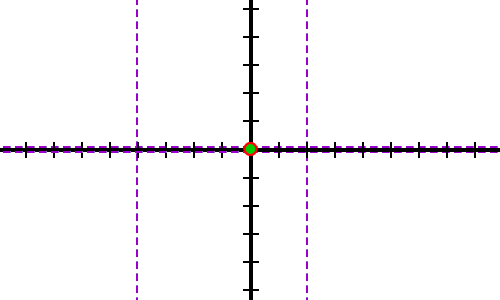
intercepts ... ( 0 , 0 ) and asymptotes y = 0 , x = 2 , and x = -4

Since we've got that pesky y = 0 horizontal asymptote, we can't use our "nowhere else" info on the x-intercepts to figure out the "upstairs" or "downstairs" stuff.  Until we have Calculus, we're going to have to humble ourselves and plot some points -- kind of!  We're going to avoid taking that pathetic trip to Sissyville by cheating a little bit... I call it "quickie plotting."

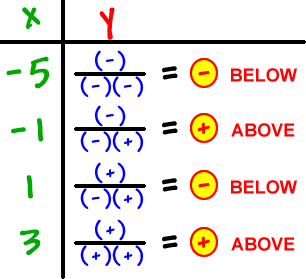
Four strategically located points will do it and all we really need to know is if he's above or below the x-axis at each point.

We'll be plugging x's into the factored form:

f ( x ) = ( 3x ) / ( ( x - 2 ) ( x + 4 ) )

*We only care about positives and negatives -- see if you can do it!



f ( x ) = ( 3x ) / ( ( x - 2 ) ( x + 4 ) )



plugging in -5 for x gives ( - ) / ( ( - ) ( - ) ) = ( - ) ... below for y, plugging in -1 for x gives ( - ) / ( ( - ) ( + ) ) = ( + ) ... above for y , plugging in 1 for x gives ( + ) / ( ( - ) ( + ) ) = ( - ) ... below for y , plugging in 3 for x gives ( + ) / ( ( + ) ( + ) ) = ( + ) ... above for y

Now we've got it! 

*Remember that he can only cross the x-axis at
x = 0... So, once he's below, he'll be stuck there...  and, once he's above, he'll have to stay above!

 

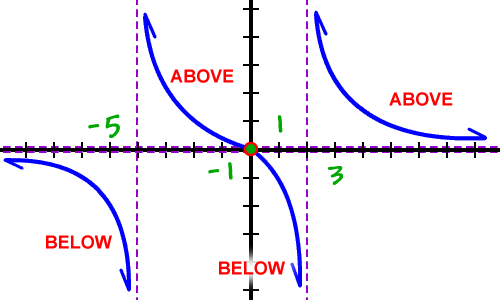
graph of f ( x ) = ( 3x ) / ( x^2 + 2x - 8 ) ... under the x-axis at x = -5 , above the x-axis at x = -1 , below the x-axis at x = 1 , and above the x-axis at x = 3
 

YOUR TURN:

Graph

f ( x ) = ( x - 3 ) / ( x^2 - 3x - 10 )

(You already have all the pieces!)

*Remember that, when you are working these things out -- write out all of your work in a neat and organized way!  This is one of the main reasons you have to take math classes -- they teach you to organize your thoughts AND TO THINK!