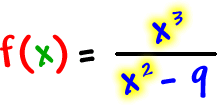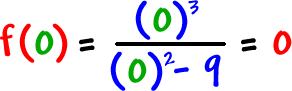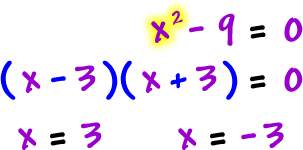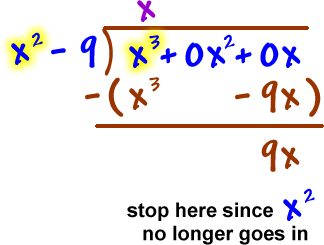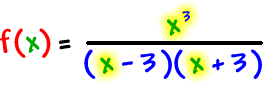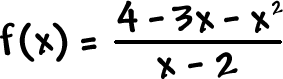One last problem:
| Graph |
|
2
things |
|
|
y-intercepts: Find
f(0) |
|
|
|
|
|
x-intercepts:
numerator =
0, solve |
|
|
|
|
|
Vertical asymptotes:
denominator =
0, solve |
|
|
|
|
|
Horizontal asymptote: |
| Look at |
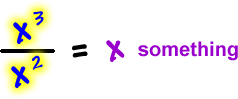 |
Hey -- it's a
slant! |
|
|
Slant asymptote: |
|
|
|
OK, Skippy -- are you ready to graph this bad boy?
Intercepts and asymptotes:
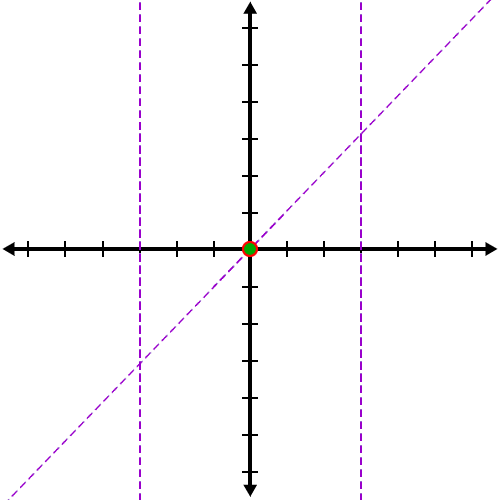
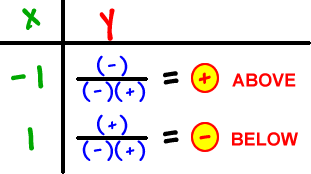
First, let's think about the left and right neighborhoods:
Here's what we've got -- see if you can figure it out!
Graphs hug asymptotes.
These guys are functions.
He can ONLY cross the x-axis at x = 0.
Can he do this?
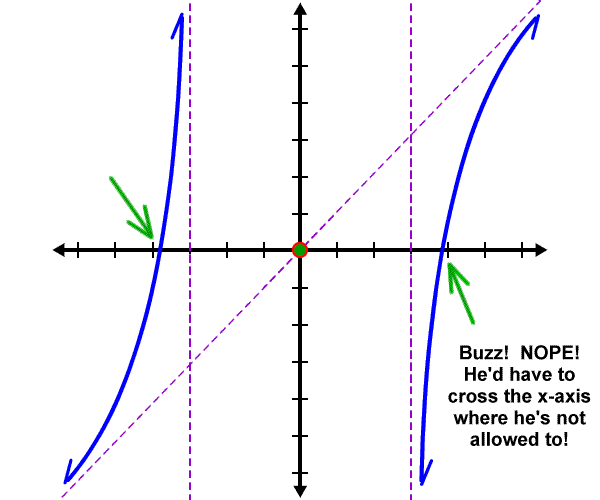
So, it must be like this:
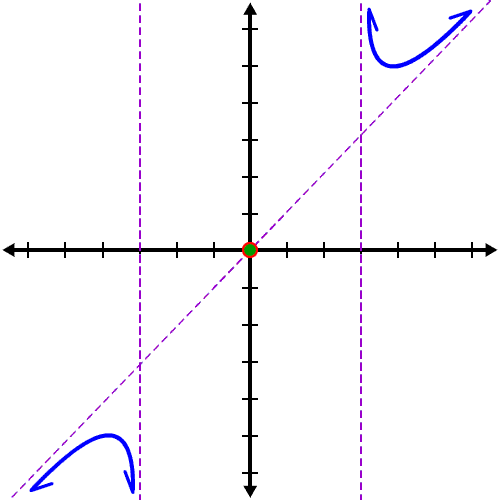
What about the middle neighborhood?
We'll need to quickie plot two points... Try it before going on.
|
|
|
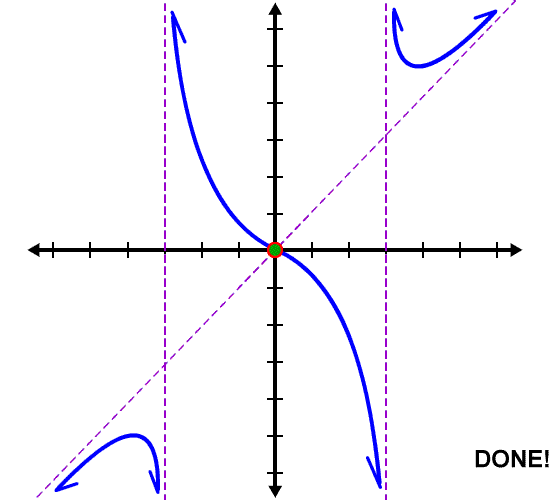
NOTE: A common mistake that students make is to think that a graph cannot cross a slant or horizontal asymptote. This is not the case! A graph CAN cross slant and horizontal asymptotes (sometimes more than once). It's those vertical asymptote critters that a graph cannot cross. This is because these are the bad spots in the domain.
YOUR TURN:
| Graph |
|