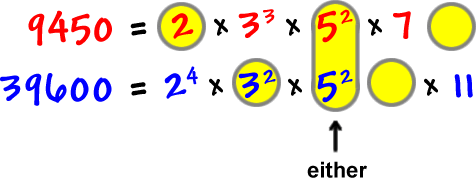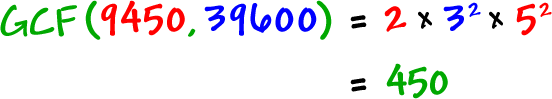Why do we need this method?

Because, with bigger numbers, there are usually way too many factors to list out!  Even though this method uses harder math, it's really more efficient.

Check it out:

Find

Do you want to find all of the factors of these guys?  I sure don't!

Here are the prime factorizations:

 

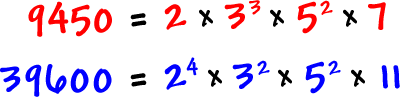
To keep things clear, I like to line up the factors:

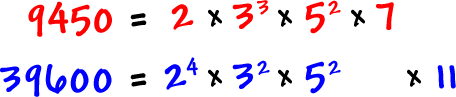
Take the lowest exponent of each (the least amount to occur in each):