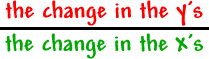1234
of 4

Slopes of Lines

Let's look at this in a way that will get us that formula for crunching slopes from two points:

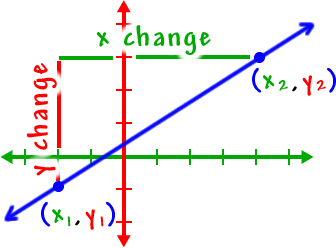Graph of a line that passes through the points ( x1 , y1 ) and ( x2 , y2 ) ... y change up ... x change overLook at the rise / run as

the change in the y's / the change in the x's

That is what gets us that familiar formula:

slope = ( y2 - y1 ) / ( x2 - x1 )

 

In math and science, we often use a Greek capital "D"... delta ( delta)...  to represent a "change".

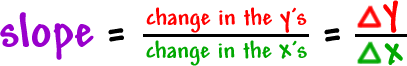
slope = ( change in the y's / change in the x's ) = ( delta y / delta x )
 

A Calculus notation you'll see a LOT ditches the Greek letter part and uses "d's"...

slope = ( change in the y's ) / ( change in the x's ) = ( delta y ) / ( delta x ) = dy / dx
 

It's a simple thing from Algebra, but the slopes of lines are going to be REALLY important in Calculus.