12345
of 5

Mathematic Induction

OK, Let's do one!

Prove

P( n ): 1 + 2 + 3 + ... + n = n( n +1 ) / 2
 

1 )

 Show P( 1 ) is true:

Stick a 1 in for all the n's and show it works.

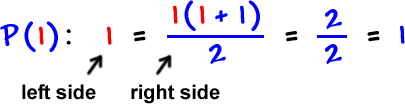
P( 1 ): 1 = 1( 1 + 1 ) / 2 = 2 / 2 = 1 ... 1 is the left side ... 1( 1 + 1 ) / 2 is the right side

So, P( 1 ) is true.


 

2 )

 Assume P( k ) is true:

Stick a k in for all the n's and say it's true.

P( k ): 1 + 2 + 3 + ... + k = k( k + 1 ) / 2
is true.

 

3 )

 Show P( k ) --> P( k + 1 )

Use P( k ) to show that P( k + 1 ) is true.

Write out your goal by sticking ( k + 1 ) in for all the n's... Leave on the left side.

GOAL: P( k + 1 ): 1 + 2 + 3 + ... + k + ( k + 1 ) = ( k + 1 )[( k + 1 ) + 1 ] / 2

Start with the left side of the P( k + 1 ) and slowly turn it into how the right side looks.

 

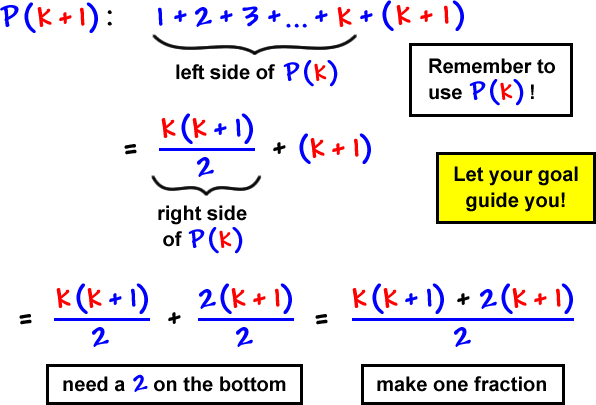
P( k + 1 ): 1 + 2 + 3 + ... + k + ( k + 1 ) ... Remember to use P( k )! ... = k( k + 1 ) / 2 + ( k + 1 ) ... Let your goal guide you! ... = k( k + 1 ) / 2 + 2( k + 1 ) / 2 = k( k + 1 ) + 2( k +1 ) / 2 ... ned a 2 on the bottom ... make one fraction


Notice that there is a ( k + 1 ) in the front of your goal, so factor that out.
 

= ( k + 1 ) + ( k + 2 ) / 2 = ( k + 1 )[( k + 1 ) + 1 ] / 2 ... just a little rewrite here

So, P( k ) --> P( k + 1 )

 

4 )

 Thus, P( n ) is true.  []

 

Whew, that looks like one big mess!  When doing a problem like this,
you need to show ALL the work I did except for my [ boxed ]  
comments.  And, yes, you have to show each of the little steps in
part 3...  Don't want to confuse the monkey!

Before we do another one, I want you to rewrite this last one out again -- but, without my comments.  Think through each step as you go.