12345
of 5

Mathematic Induction

TRY IT:

Prove

P( n ): 1 + 3 + 5 + ... + ( 2n - 1 ) = n^2

OK, here's a different type...  Same process, it just works differently because it's a different kind of formula to prove.  It's one of our old algebra buddies!

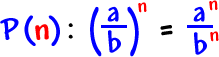Prove P( n ): ( a / b )^2 = a^n / b^n

 

1 )

 Show P( 1 ) is true:

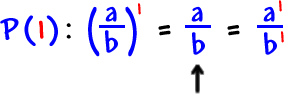
P( 1 ): ( a / b )^1 = a / b = a^1 / b^1
A picky but important note is that you can't skip this middle step. If you do, then you'd be using the rule you are trying to prove... which is circular reasoning.

So, P( 1 ) is true.

 

2 )

 Assume P( k ) is true:

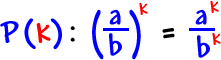P( k ): ( a / b )^k = a^k / b^k is true

 

3 )

 Show P( k ) --> P( k + 1 )

Use P( k ) AND P( 1 ) to show that P( k +1 ) is true.

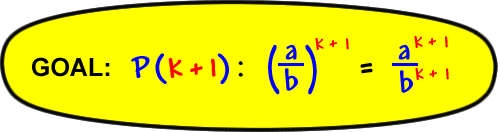
GOAL: P( k + 1 ): ( a / b )^( k + 1 ) = a^( k + 1 ) / b^( k + 1 )

Start with the left side... Use P( k ) and P( 1 ) show every little step... Don't confuse the monkey... End up with the right side.
 

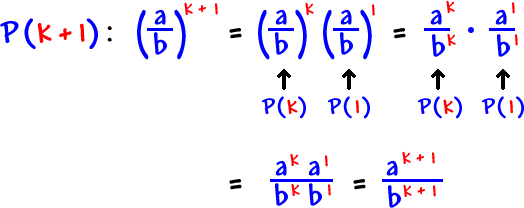
P( k + 1 ): ( a / b )^( k + 1 ) = ( a / b )^k * ( a / b )^1 = a^k / b^k * a^1 / b^1 = a^k * a^1 / b^k * b^ k = a^( k + 1 ) / b^( k +1 )

 

So, P( k ) --> P( k + 1 )

 

4 )

 Thus, P( n ) is true.  []

Write this guy out without my comments.  Think about each step!

TRY IT:

Prove

P( n ): ( ab )^n = a^n * b^n