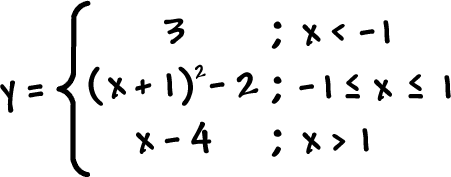12
of 2

Piecewise Functions

Let's do one with three pieces...

Graph

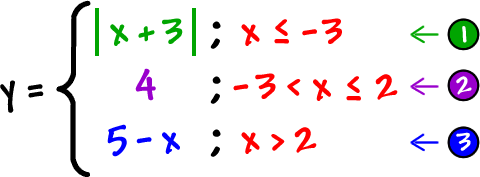
y = | x + 3 | for x is less than or equal to -3 , y = 4 for -3 < x which is less than or equal to 2 , and y = 5 - x for x > 2

Let's put up the fencing:

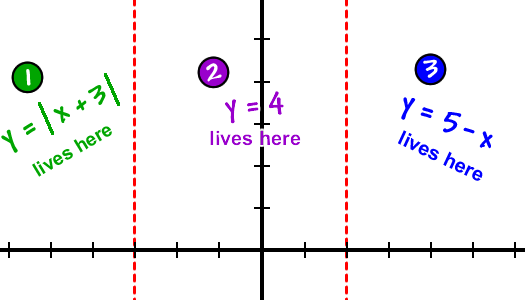
Put up fences at x = -3 and x = 2 ... y = | x + 3 | lives on the left , y = 4 lives in the middle , and y = 5 - x lives on the right

Remember that they can't cross over into the other neighborhoods!

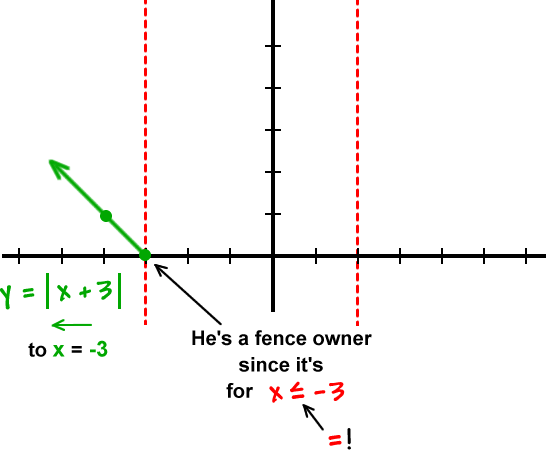
Graph of y = | x + 3 | on the left of the graph ... shifted left to x = -3 ... He's a fence owner since is for x is less than of equal to -3 ... = !

 

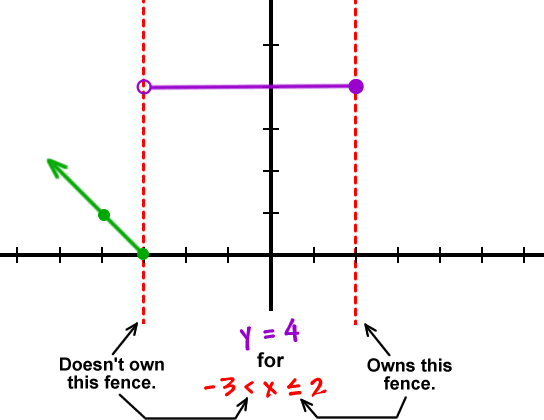
Graph of y = 4 in the middle section ... -3 < x which is less than or equal to 2 ... doesn't own the left fence, owns the right fence

 

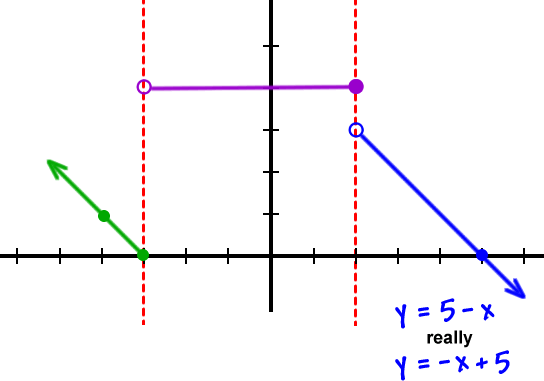
Graph of y = 5 - x ( really y = -x + 5 ) in the right section ... not a fence owner

OK, so why are we being so careful about not crossing the fences into the other neighborhoods?

Because these guys are functions!  Remember that functions have to pass the vertical line test.

TRY ONE:

Graph

y = 3 for x < -1 , y = ( x + 1 )^2 - 2 for -1 is less than or equal to x which is less than or equal to 1 , and y = x - 4 for x > 1