1234
of 4

Real Zeros

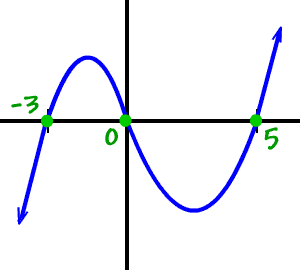
Let's do a couple more.

Find the real zeros of

f ( x ) = x ( x - 5 ) ( x + 3 )

then draw a rough sketch of the graph:

What's his basic shape?

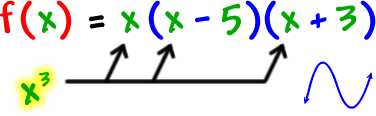
f ( x ) = x ( x - 5 ) ( x + 3 ) ... the first terms multiply together to give x^3 ... basic cubic shape

What are the real zeros?

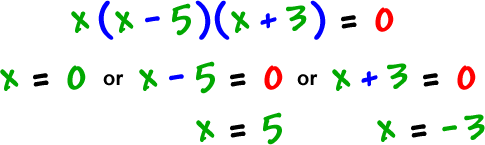
x ( x - 5 ) ( x + 3 ) = 0 gives x = 0 or x - 5 = 0 or x + 3 = 0 which gives x = 0, x = 5 and x = -3

real zeros: -3, 0, 5

Let the basic shape guide you!

basic shape of a 3rd degree polynomial

 

 

*If you take Calculus, you'll learn a very cool and very easy way to find out how high the mountains are and how low the valleys are.

YOUR TURN:

Find the real zeros of

f ( x ) = x ( x - 2 ) ( x + 4 ) ( x - 6 )

then draw a rough sketch of the graph: