1234
of 4

Real Zeros

This one has a twist...

Find the real zeros of

f ( x ) = x ( 5 - x ) ( x + 3 ) ( x - 1 ) ( x + 7 )

then draw a rough sketch of the graph:

Do you see the twist?  It's the (5 - x) guy!

So, what's his basic shape?

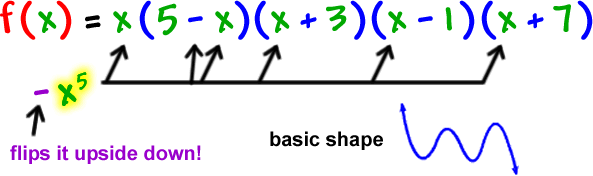
f ( x ) = x ( 5 - x ) ( x + 3 ) ( x - 1 ) ( x + 7 ) ... the x terms give -x^5 ... the graph will be an upside down 5th degree polynomial

What are the real zeros?

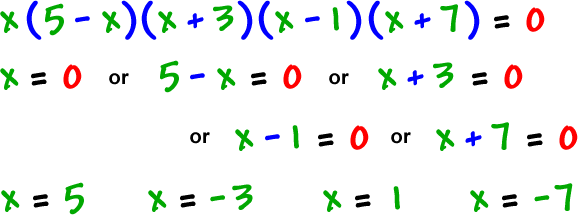
x ( 5 - x ) ( x + 3 ) ( x - 1 ) ( x + 7 ) = 0 gives x = 0 or 5 - x = 0 or x + 3 = 0 or x - 1 = 0 or x + 7 = 0 which gives x = 5 , x = -3 , x = 1 , and x = -7

real zeros: -7, -3, 0, 1, 5

 

TRY IT:

Find the real zeros of the functions and draw a rough sketch of the graph:

f ( x ) = ( x - 3 ) ( 6 - x ) ( x + 2 )

f ( x ) = x ( x - 3 ) ( 2 - x ) ( x + 5 )