1234
of 4

Multiplicities

These powers are called multiplicities.

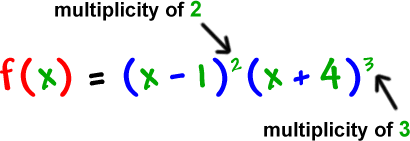
f ( x ) = ( x - 1 )^2 ( x + 4 )^3 ... ( x - 1 ) has a multiplicity of 2 and ( x + 4 ) has a multiplicity of 3

Let's do another one:

Find the real zeros of

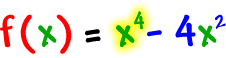
f ( x ) = x^4 - 4x^2

then draw a rough sketch of the graph:

What's the basic shape?

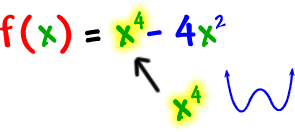
f ( x ) = x^4 - 4x^2 ... basic 4th degree polynomial shape

What are the real zeros?

Solve    f ( x ) = 0

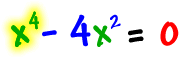
x^4 - 4x^2 = 0

We just need to do a little factoring...

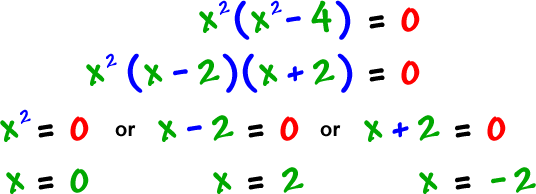
x^2 ( x^2 - 4 ) = 0 gives x^2 ( x - 2 ) ( x + 2 ) = 0 which gives x^2 = 0 or x - 2 = 0 or x + 2 = 0 which gives x = 0 , x = 2 , and x = -2

real zeros: -2, 0 (kiss), 2
                multiplicity of 2

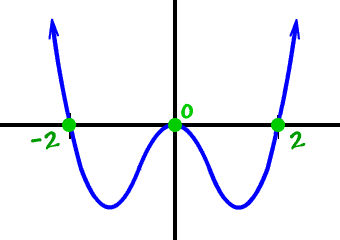
graph of f ( x ) = x^4 - 4x^2

Why don't you check this guy on the graphing calculator?

Enter it as  x^4-4x^2

(Your window may still be weird from the last guy we graphed...  hit the RESET button on the calculator to fix it.)