1234
of 4

Multiplicities

YOUR TURN:

Find the real zeros of the following functions and, then, draw a rough sketch of the graph:

f ( x ) = x ( x - 3 )^2 ( x + 5 )

f ( x ) = ( x - 4 )^2 ( x + 1 )

Now let's try this one:

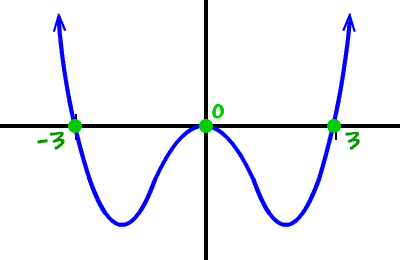
We want to graph a fourth degree polynomial that has real zeros of

-3, 0 (multiplicity 2), 3

It's a 4th degree...  So, the basic shape is

standard shape for a 4th degree polynomial

Or we could even go with

general shape for an upside-down 4th degree polynomial

(No one said it wasn't up-side-down!)

The zeros at -3 and 3 are shoot throughs...  and the zero at 0 is a kiss...

graph of a 4th degree polynomial that has real zeros of -3 , 0 ( multiplicity 2 ) , 3

YOUR TURN:

Graph a fifth degree polynomial that has real zeros of

-6 (mult 2), -1, 3 (mult 2)

Also, can you write out the official f(x) formula for him?