The graph of  g(x) = sin(10x)  is getting squished (or damped) between the graphs of  y = x  and  y = -x !!

Don't believe me? Then check it out! Let's graph  f(x) = x*sin(10x), 
y = x and   y = -x  all on the same graph...

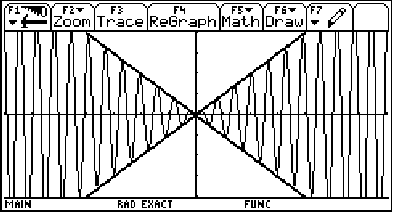
(y=x and y= -x are the thicker lines.)

We see that our sine graph is, indeed, bounded between them! Pretty cool, huh?

In the function

this x is called the damping factor.

Let's try something more complicated.

What would the graph of  f(x) = (log x)*cos(15x) look like?

Well,   g(x) = cos(15x)  looks like:

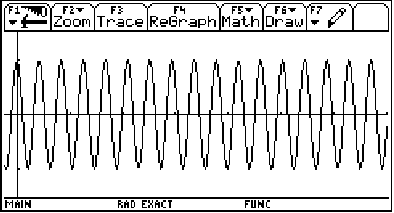
(graphing window: x on [-.235, 7], y on [-1.5, 1.5])

Our damping factor is  log x. So,  g(x) = cos(15x) is going to get bounded by  
y = log x  and  y = -log x . (Note that g(x)=cos(15x) is also going to get restricted to the domain of y=log(x) which is x>0.)

Let's see what it will look like!

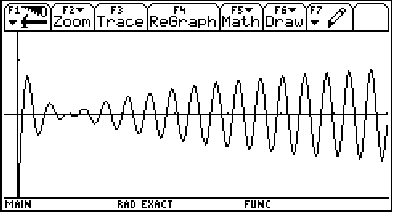
(graphing window: x on [-.235, 7], y on [-1.5, 1.5])

It sure looks like it's bounded by those logs... Let's graph them to be sure!

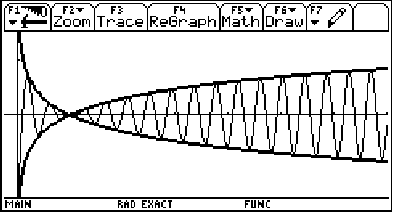
Yep! (Looks like the messy end of a fish, doesn't it?)