Logarithmic Fades:

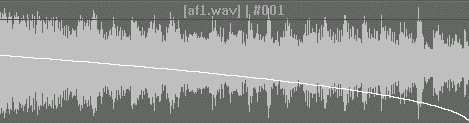
This type of fading is often a favorite of engineers because of the natural sound it produces. Here's what Autumn Fell sounds like with a logarithmic fade. Can you tell the difference? See if you can by comparing it to the slower linear fade. You can hear the music in the log fade a lot longer.

Can you figure out the mathematics behind the logarithmic fade? How would we graph an example?

Let's do some reviewing and exploring.

If we graph 

 ,   and   ...

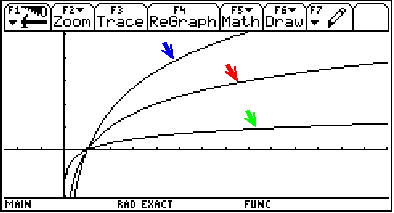
(Graphing window: x on [-2.58, 13.98], y on [-2, 5.1])

Notice that the smaller the base (3/2, 2 and 10 in our example), the steeper the graph.

Now, how can we get our logs to flip over the y-axis like they are in our fades? By using f(-x) instead of f(x)!

Let's check by graphing  

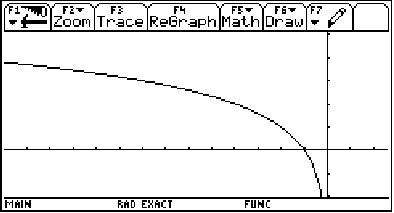
(Graphing window: x on [-13.98, 2.38], y on [-2, 5.1])

Getting back to our logarithmic fades... When the engineer decides how fast the song should fade, the program adjusts the base of the logarithm!

Music is just applied mathematics...
A good musician is an applied mathematician!

Eddie Van Halen? Math geek? You be the judge!