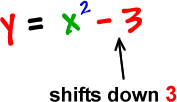
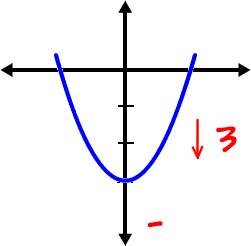
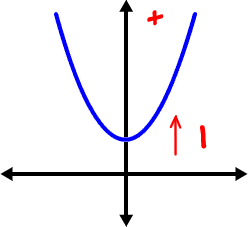
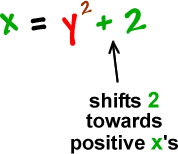
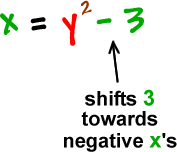
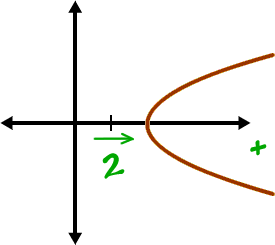
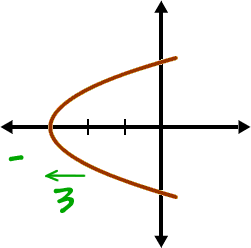
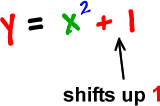12345
of 5

Sideways Parabolas

Finally, we've got the shifts that are hanging off on the end:

Standard Parabola Guy:

y = x^2 - 3 ... shifts down 3

y = x^2 + 1 ... shifts up 1


*Shifts 3 towards negatives!


*Shifts 1 towards positives!


y = x^2 - 3 ... standard parabola shifted down 3 (towards negative y's)


graph of y = x^2 + 1 ... standard parabola shifted up 1 (towards positive y's)

y = x^2 + k
These go together...

y is an up-n-down guy,
so k is an up-n-down shift.

(

Some people actually write the graphing form this way to really lock them together:
( y - k ) = a ( x - h )^2

)

Sideways Parabola Guy:

x = y^2 + h
These go together...

x is a back-n-forth guy,
so h is a back-n-forth shift!

(Remember I'm only doing quick rough sketches.)

x = y^2 + 2 ... shifts 2 towards positive x's

x = y^2 - 3 ... shifts 3 towards negative x's


graph of x = y^2 + 2 ... sideways parabola shifted 2 to the right (towards positive x's)


graph of x = y^2 - 3 ... sideways parabola shifted 3 to the left (towards negative x's)

 

TRY IT!:

Graphx = y^2 - 4